Authors: brilliant predecessors in my interpretation.
Composed by VVvv. Translated by Google translate, ran by VVvv.
Thanks are given to professors Jiri Bicak and Michal Krizek.
Version Tenerife – Miraverde, October 16, 2021
Translated December 8, 2022
We consider a hypothetical model of space-time with spatially constant curvature, which expands equally at every point in space, because there is no EXCEPTIONAL place in it where anything can happen differently. I call this kind of expansion the ECSTASY of space. It means that the SUBSTITUTIVE CIRCLE, which substitutes a straight direction in a uniformly curved space, will increase its radius R with time t, dR/dt= ΔV0 >0.
The distance of objects from us z=R·φ, where R is the radius of curvature and the angle φ is measured in an arc measure with the origin at the point of observation, will not grow at the rate ΔV0, but at the rate dz/dt= dR/dt·φ, or ΔV=ΔV0·φ. Therefore, the increase in the observed speed of objects receding with the distance φ from us observers is an inherent property of the model.
By increasing the angle φ, we reach the limit situation, i.e. ΔV=c, where c is the speed of light propagation. This is a consequence of the model, and I call that limit the LIGHT BARRIER of the Universe (SBV). In physics, it is best matched by established terms such as the cosmological horizon or the Horizon of the Universe (HV), or the limit of the observable Universe from the observer’s point of view.
The term AGE of UNIVERSE (VV) is introduced as the time of light’s flight to us from this distance HV≡ SBV= c·VV, and the term Observable SIZE of UNIVERSE RPV, as the distance to which the space was carried away by ECSTASY from us in all directions at a speed of ΔV0 during that time, RPV= ΔV0·VV. Since the farthest object observed along a circular arc can never lie further than on the opposite side of the circle from the observer φ= π, then the corresponding SIZE of UNIVERSE comes out as Rv= R·π.
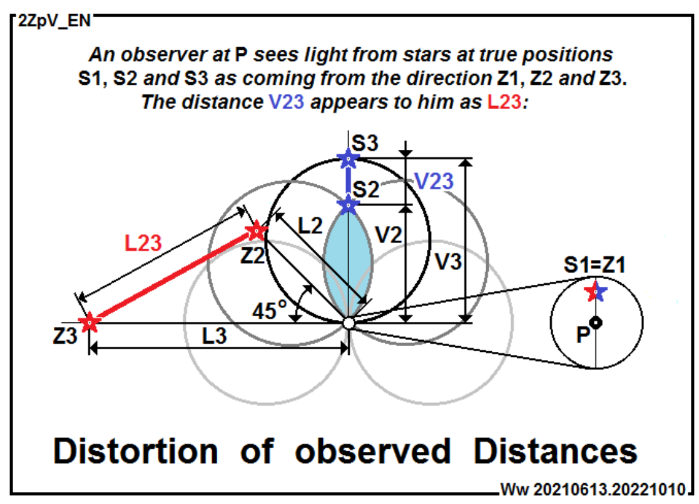
Another consequence that the model draws our attention to is that we observe distances between objects in the distant Universe greater than they are in space. This distortion of our observation is the reason why there seems to be a lack of gravity in the distant Universe, as if there is a GRAVITY DEFICIT. This is made visible, for example, by the figure Distortion of Observed Distances [2ZpV_EN], which combines all 3 sketches from the figure STARS and LIGHT PROPAGATION G [2phG_EN] from the first part of this file into one:
The situation is simplified by considering the drawn stars “S1“, “S2” and “S3” as existing simultaneously by stopping the flow of time, thus freezing their positions in space-time. Although, for example, the light flew from S2 to us observers at point “P” along an arc distance L2=R·π/2 and from S3 a distance twice L3=R·π (R is the radius of curvature of space), and thus we actually observe the star S3 in a double past than the S2 star, we consider their positions by freezing the course of time in space unchanging.
Comparing the observed distance L23 and the actual distance V23 gives L23/ V23≈ 3,95. Thus, the distorted L23 distance is almost four times larger (!) than the true V23 distance, and thus the corresponding mutual gravitational effect would be almost sixteen times weaker (!!) for this situation. Similarly, for the star S1, which is so close to us (L1≈V1≈0) that we consider the influence of the curvature of space on its observation still negligible, the ratio of the distorted to the real distance will be L12/V12≈ 1,11. Due to the distortion, the observed distance also increased, but only slightly by approximately 11% compared to the actual distance.
Although we considered the special case of observing objects from us in a straight line behind one another, and by freezing the passage of time we limit its validity to mutual distances significantly smaller than the radius of curvature of space, and the speed of their changes in position in space significantly smaller than the speed of light, we showed that as the model predicts an amplifying effect of increasing mutual distances between observed objects as their distance from us increases.
This could point to a hitherto misinterpreted curvature effect, which may have required so-called dark matter to be introduced to compensate for the missing gravity. That is, some invisible matter, the amount of which is estimated in the quote https://en.wikipedia.org/wiki/Dark_matter to be approximately 85% of the matter in the universe. That is, such a large amount that only 15% (!!!) of observable “light matter” would be left in the Universe.
In conclusion, the second challenge is presented: to determine the consequence of the distortion of the mutual distances that the model predicts, in specific situations, and thus also to determine the size of the GRAVITY DEFICIT. It would be verified to what extent the observed lack of gravity is due to the predicted distortion of the observed mutual distances.